How far away should you rent?

The value of your rent is influenced heavily by location: how easy you can get to where you need to be. For understanding this, we need a model of time valuation.

Time valuation

Let's find a way to value the extra time spent past the 8 hours, for getting to work.

Constraints

• Suppose you have a monthly salary of 1 unit (which we can later swap for an actual amount).
• Suppose you work for 8 hours a day (full-time in most countries).
• Suppose you are not willing to give away 16 hours a day, no matter what your salary would become. 
• This means your salary would have to reach infinity in order for you to accept it.

We need to construct a function out of this:

• It must go through (0, 0) - this means for no work, you get no pay. 
• It must go through (8, 1) - for 8h of work, you get 1 unit.
• It must have a vertical asymptote going to positive infinity at x=16 - your time becomes infinitely precious when you have no more of it.

Function

A somewhat handy function which goes through (0, 0) and asymptotes up at π/2 is the tangent function. You can use whichever function is most suited for your needs, there is no guarantee that the tangent actually maps to your exact preference - it is only accurate in those three specified points (0, 8 and 16).
Edit: In particular, you can check out the inverse logistic function (logit - which may be a better fit). 

We need to stretch and condition the tangent function as follows:

• We want the infinity to happen at 16, not at π/2. Therefore, instead of tan(x) we will use tan(x * π/32).
• We then want the value at 8 to be exactly 1. Therefore, we divide the the function by its value at 8h:
• tan(x * π/32) / tan(8 *π/32) = tan(x * π/32) / tan(π/4)
• however, tan(π/4) is already 1, so we don't need to divide at all
• so, the final function is tan(x * π/32)
• We then avoid looking at the values outside the inverval [0, 16], because:
• we are not willing to work negative hours (would that mean hiring someone to do your job? heh)
• we are not willing to work more than 16 hours
• we have not checked that the function corresponds to our wishes outside of the 3 points we have just defined

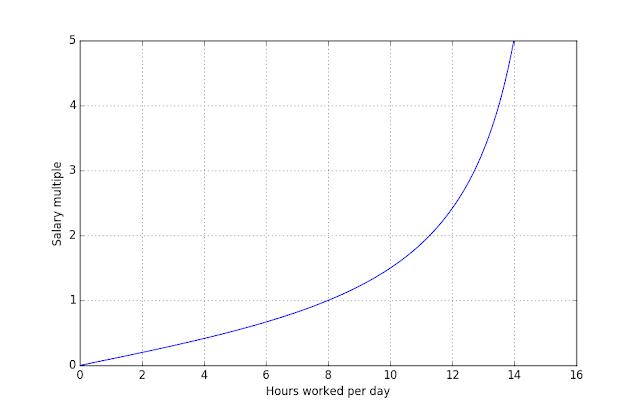
Here is what this function looks like:

Note the dramatic increase: if you spent two extra hours commuting each day (8h -> 10h), you might as well ask for a 50% increase in your salary - because that is what this valuation says your added time is worth. This is in contrast to asking proportionally (25% more) if you were to be paid the same hourly rate.

This increase is caused by your time availability: the more time you spend working, the more valuable your free time is, because there's less of it!

Of course, your preference might not have the same steepness as this function, which means you should customize this function according to your preference.

• Perhaps you don't mind spending 10 hours for work, which means you should extend the linear-ish portion further from 8h to 10h. 
• Note that when you halve your free time (work 12h), the salary you should ask according to this function is about 2.5 times greater (not 2 times, and not 1.5 times as a linear hourly rate would say). This may or may not correspond to your actual preference.

But the general shape should stay the same, since the assumptions we made for the constraints seem fine to me.

More ideas you can try out:

• Different valuation functions
• Adjust for weekends - to do this, it's easier to consider the hours spent on a weekly basis, instead of daily as we did.

Rent & commute

Great, now we have a time valuation. Now, how does this fit with the rent to pay?

Suppose you had two options: 

• an apartment a step away from your office, or telecommute (commute time zero)
• an apartment 30 minutes away by whichever means of transport you use (daily commute time of 1 hour)

According to the valuation, that extra hour spent commuting costs you tan(9 * π/32) - tan(8 * π/32) worth of free time, which is about 0.2185 of your salary.
This means it should be indifferent to you to do either of the following:

• pay 21.85% of your salary extra to live at the office
• or to commute for 1 hour each day

This amount, multiplied by the mean salary in Romania (487.93 euros), yields 106.6 euros.

So, suppose you pay 200 euros for the apartment half an hour away. Then, you might want to pay 306.6 euros for the one right at your office.

Notice that this difference is a hefty amount (more than a fifth of the salary). This is because your time is limited, and due to the way the tangent grows to infinity.

Important caveat in this analysis

This model overlooks something critical: are your new costs letting you save enough money? Suppose right now you spend 80% of your salary. If you were to make the choice of moving to the office (an expensive rent nearby), and pay 21.85% for rent, you would be net negative, which would of course be unacceptable.

So, it seems there is one more valuation to consider: that of money. This raises a question; how great is one's preference of money, compared to time?

I might explore this in a later blog post, but now, I have no more...

...time!

 Edit (2023-05-16):

  A book might provide the optimal amount of spending you should do during your life: Die With Zero. Feel free to integrate it with the rest of the information from this post.